Spreading points on a disc and on a sphere

When working with computer graphics, machine vision or simulations of various kind, two problems (among many others) which keep popping out are

• How to have N points approximately evenly distributed over a disc
• How to have N points approximately evenly distributed over a sphere

One way to build a solution for those two problems is to rely on a particle system. Each point is a particle, particles are repulsing each other with a \( \frac{1}{r^2} \) force. Put the particles on the disc or the sphere surface, at random locations. Shake vigorously the particles, add some small drag force, let the particles reach a steady state, shake again ... rinse, repeat. It is not as easy as it sounds. How to setup the forces ? How to handle the boundary of the disc ? Which integrator to use to compute the particle's motion ? And for more than a few hundred particles, it will be terribly slow.

Spirals

There are much simpler and leaner algorithms to evenly distribute N points over a disc or a sphere, if one can live with just a good approximation. The main idea fits in one word : spiral ! Let's start with a disc. Imagine a spiral of dots starting from the center of the disc. In polar coordinates, the N points are produced by the sequence

\[ \rho_i = \theta i \]

\[ \tau_i = \sqrt{\frac{i}{N}}\]

\( \rho_i \) and \( \tau_i \) are respectively the angle in radian and the radius of the i-th point. Why \( \tau_i = \sqrt{\frac{i}{N}} \) ? Let's try to cut a unit disc in one disc and one ring of equal areas, by cutting the unit disc at radius \( r_c \). The small disc and the ring are of equal areas, thus \( \pi r_{1}^2 = \pi - \pi r_{1}^2 \). Thus \( r_1 = \sqrt{\frac{1}{2}} \). Now, let's try to cut the unit disc in one disc and 2 concentric rings, all of equal areas. A slightly more complex calculation (a system of 2 linear equations) would tell us that we should cut the unit disc at radius \( r_1 = \sqrt{\frac{1}{3}} \) and \( r_2 = \sqrt{\frac{2}{3}} \). The calculation is a more complex when cutting the unit disc in N equal areas rings, but you can guess the answer now : \( r_1 = \sqrt{\frac{1}{N}} \), \( r_2 = \sqrt{\frac{2}{N}} \), \( r_i = \sqrt{\frac{i}{N}} \).

What about the ideal \( \theta \) ? Brace yourself... This is the golden angle, \( \pi (3 - \sqrt{5}) \) ! It's roughly equal to 137.508°, or about 2.39996 radians. The golden angle is the "most irrational" angle, defined as \( 2 \pi (1 - \frac{1}{\phi}) \) with \( \phi \) being the golden ratio. If \( \theta \) is a rational number, we would obtain clusters of points aligned with the center of the disk. Thus \( \theta \) have to be irrational. As it turns out, the golden ratio is the irrational number the hardest approximate with a continued fraction. Written as a continued fraction, the golden ratio is the irrational number with the slowest convergence of all the irrational numbers. The golden angle gives the best possible spread for the \( \rho_i \) angles. This method to spread points over a disc is called Vogel's method.

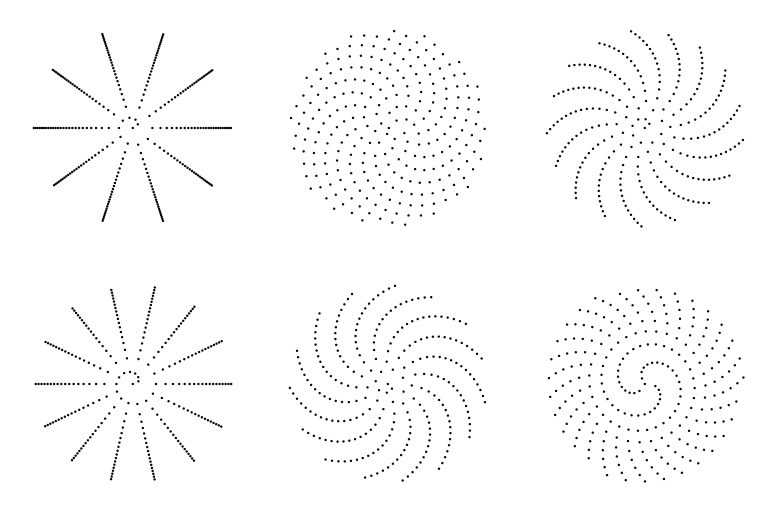
Vogel's method is dead simple to implement. In pure, barebone Python, it can be done like this

import math

n = 256

golden_angle = math.pi * (3 - math.sqrt(5))

points = []
for i in xrange(n):
  theta = i * golden_angle
  r = math.sqrt(i) / math.sqrt(n)
  points.append((r * math.cos(theta), r * math.sin(theta)))

Using numpy, one can use vector operations like this

import numpy

n = 256

radius = numpy.sqrt(numpy.arange(n) / float(n))

golden_angle = numpy.pi * (3 - numpy.sqrt(5))
theta = golden_angle * numpy.arange(n)

points = radius[:,None] * numpy.stack([numpy.cos(theta), numpy.sin(theta)])

Spheres

What about the sphere ? We can reuse the golden angle spiral trick. In cylindrical coordinates, we would generate N points like this

\[ \rho_i = \theta i \] \[ \tau_i = \sqrt{1 - z_{i}^2} \] \[ z_i = \left(1 - \frac{1}{N} \right) \left(1 - \frac{2i}{N - 1} \right) \]

And voila, an extremely cheap method to spread point evenly over a sphere's surface ! The code for this method is very close to the one for Vogel's method.

n = 256

golden_angle = numpy.pi * (3 - numpy.sqrt(5))
theta = golden_angle * numpy.arange(n)

z = numpy.linspace(1. - 1. / n, 1. / n - 1., n)
radius = numpy.sqrt(1. - z ** 2)

points = numpy.stack([radius * numpy.cos(theta),
                      radius * numpy.sin(theta),
                      z], axis = 1)

Note that you can also use this method to make a sphere mesh. The sphere will look good even with few polygons, but the indexing and computing the normals won't be especially fast. For this specific problem, making a sphere mesh, Iñigo Quilez have a very nice, efficient method introduced here.

I made ready-to-use Python functions on Github for the disc and the sphere.